
Outliers in linear regression
Modeling and inference
Outliers in regression
Outliers are observations that fall far from the main cloud of points.
-
They can be outlying in:
- the \(x\) direction,
- the \(y\) direction, or
- both.
However, being outlying in a univariate sense does not always mean being outlying from the bivariate model.
Points that are in-line with the bivariate model usually do not influence the least squares line, even if they are extreme in \(x\), \(y\), or both.
Outliers and influence
- A: One outlier in the \(y\) direction, also outlying in the bivariate model; slightly influences the regression line.
- B: One outlier on the right (outlying in \(x\) and \(y\), but not outlying in the bivariate model); close to the regression line and not influential.
- C: One point far from the cloud (outlying in \(x\), \(y\), and bivariate model); pulls the regression line upward, worsening fit for the main data.
Outliers and influence
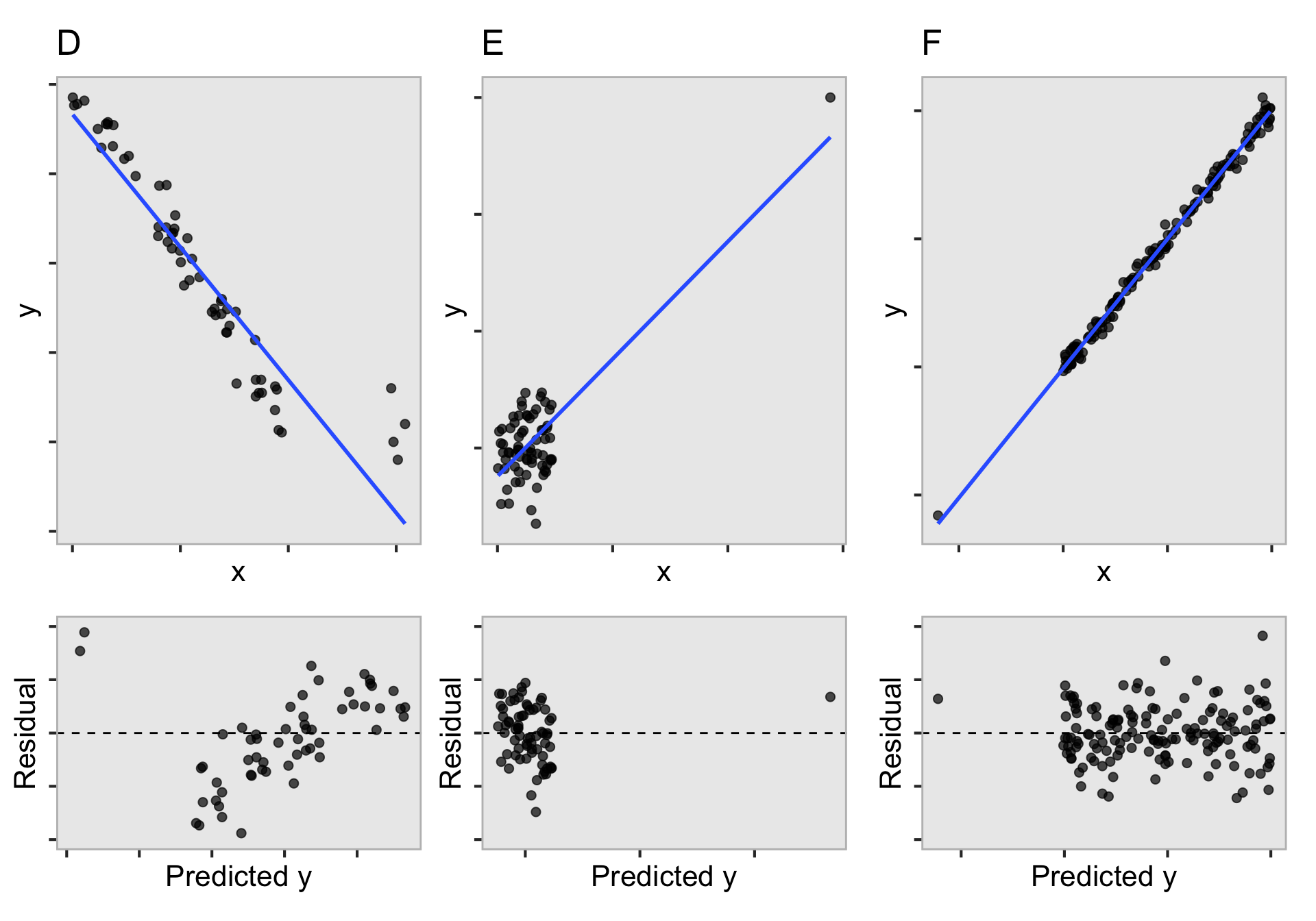
- D: A secondary small cloud of four points (outlying in \(x\) and bivariate model); strongly influences the regression line, creating poor fit.
- E: Outlier far right (outlying in \(x\) and \(y\)); the regression line is largely controlled by this single point, imposing a trend where there is none.
- F: One outlier far away (outlying in \(x\) and \(y\)), but in-line with the model; has little influence.
Types of outliers
Outliers: Points or groups of points that stand out from the rest of the data.
Leverage points: Points that fall horizontally away from the center of the cloud tend to pull harder on the line, so we call them points with high leverage or leverage points.
-
Influential points: Outliers, generally high leverage points, that actually alter the slope or position of the regression line.
- We say a point is influential if omitting it would substantially change the regression model.
Practical advice
Test your analysis with and without outliers.
Compare and discuss the impact of outliers on model fit.
Present both models to stakeholders to choose the most reasonable interpretation.
Warning
Removing outliers should only be done with strong justification – excluding interesting or extreme cases can lead to misleading models, poor predictive performance, and flawed conclusions.